正确彻底消灭蚰蜒的方式
蚰蜒生活在阴湿地方,以蜘蛛、臭虫、白蚁、蟑螂、蠹鱼、蚂蚁和其它居家节肢动物为食,有益环境,不是害虫。所以,彻底杀灭的方法不是杀掉它们。而是搞好卫生。室内没有食物了它们自然就走了。
蚰蜒有毒,而且毒颚很大,会咬人,能分泌毒液,触及人体皮肤后即可致局部疱疹,让人刺痒难忍。所以在被蚰蜒咬到之后要及时就医,所以蚰蜒一定要彻底消灭感觉!不过虽然蚰蜒有毒,但却并不是“五毒”之一,民间常说的“五毒”分别是蜈蚣、毒蛇、蝎子、壁虎和蟾蜍这五种,蚰蜒并非其中之一。

在阴暗潮湿处喷洒敌百虫粉剂、灭害灵等卫生喷射剂,家里潮气大,或者是家里环境卫生比较差。想要彻底根除这种情况,一定要保持家里的环境干净卫生,地上有水要及时的清除,如发现墙角有泛潮的情况应该买些干燥粉,洒在泛潮的地方。
家里出现了蚰蜒可以去超市买瓶杀虫剂在屋里的每个角落喷一喷,喷之前关好门窗,喷完后屋里不要留人,可以出去玩半天,回来后打开门窗,家里吓人的虫子基本都杀死了。
可以在墙面涂刷杀虫涂料,但不推荐,因为有化学药剂残留,同时刷涂后应暂缓入住,保证足够通风,待房内无药剂味道后再入住。
彻底清除蚰蜒的方法:
1、蟑螂药清除法,在蚰蜒经常出没的地方撒下蟑螂药,可以起到清除蚰蜒的作用。
2、杀虫喷剂清除法,在蚰蜒经常出没的地方喷撒杀虫喷剂,可以起到清除蚰蜒的作用。
3、食物链清除法,在蚰蜒经常出没的地方饲养小鸡,小鸡很喜欢吃蚰蜒,可以起到清除蚰蜒的作用。
4、找我们奔奔虫控公司,保管你药到病除 彻底消灭蚰蜒!
标签:

190
秦时明月罗网刺客原来分为八个等级,吴旷只是第二级杀手 《秦时明月》动画第五部君临天下66集更新,这一集的剧情可以说非常精彩!尽管惊鯢和掩日的身份还没有公开,但是金先生...

62
看石家庄南三条的发展和兴衰 一九九二年七月第一次来到石家庄,当时的石家庄南三条基本位于胜利大街上,从槐安路南边的老胜南汽车站到和平路之间,都是卖东西的,可以说从南三...

59
金钟国郑素英最终是否在一起 秀大腿肌肉分享健身食谱 金钟国是韩国著名的艺人,在我国的人气也非常高。在《Running Man》中,他曾被节目组安排和郑素英相亲,但是这都是为了录制节...

161
黄赌毒泛滥的柬埔寨,究竟有多乱? 柬埔寨,这片历史悠久的土地,承载着古老文明的沉淀,却也受到了现代社会的巨大冲击。这个国家,位于中南半岛,地理位置特殊,正因如此,它...

106
澳洲邀请赛第二日四排战:4AM近乎屠榜,韦神上演决赛圈个人天秀 澳洲邀请赛第二比赛日,4AM表现出色,近乎屠戮各大榜单。 队伍总积分1955位列榜单第二,队伍总击杀41个位列榜单第...

191
周润发 周润发是一位备受尊敬的华语电影男演员、摄影师,同时也是国家一级演员。他出生于1955年5月18日,成长于中国香港南丫岛,祖籍广东省江门市开平市。他的职业生涯始于1976年...

128
有些人可能不知道就进了富士康黑名单,赶紧看看吧! 作为富士康的一名14年的资深老员工,今天和大家讲讲哪些人会进富士康的黑名单。 可能有些人并不了解富士康的黑名单的意义!...

82
影片《暴裂无声》最后小男孩之死 今天刚看了暴裂无声,不得不说是一部很好的电影,大胆叙事方式,也感觉更像一部个人英雄主义影片,呵呵!可想影片里哑巴旷工一个人单挑十几个...
63
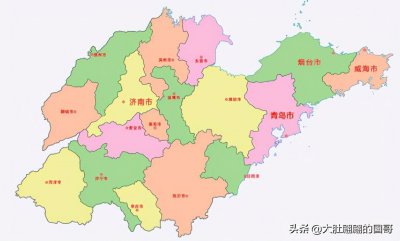
山东省各个地级市的人民是怎么看山东省的?(1) 山东省各个地级市的人民是怎么看山东省的 地图 鲁西区域 济南人眼中的山东省: 我是省会,我是老大!你们都是小老弟;那个青岛...
112
卢本伟疑似与赵梦玥和平分手,且称双方近年始终经济独立? 当初55开被全网封杀,UU对他倒是不离不弃,经常还发微博秀恩爱。 因此许多网友都把UU和55开奉为坚贞不渝的爱情。 但其...
56
刘若英的书单 刘若英(奶茶)一直给粉丝们的直观感受就是温柔,温柔,如同水一般柔。刘若英(奶茶)写过哪些书籍? 《爱情限量版》 描述了一个恋爱中的女生在旅行中不断对自己...

69
荔湾广场八副棺材来历揭晓 荔湾广场灵异事件是真的吗 很多喜欢关注灵异奇闻的人应该都听说过荔湾广场的故事。据说这个地方很诡异,曾经有许多人都在这里跳楼自杀,以至于网上...

285
军分区司令与团长,谁级别更高? 军分区司令与团长相比,在军队的行政级别上,军分区司令员的级别更高。军分区司令通常对应正师级,而团长是正团级。因此,从级别上讲,军分区...
201
呼伦湖号901型综合补给舰 901型综合补给舰是中国人民解放军海军的大型综合补给舰,是专门为航母编队建造的中国第一艘超过40000吨级的补给舰,比正在批量建造的903型整整大一倍,航...

186
30岁之前真的不要进厂打工,否则你会后悔当初的选择有多么愚蠢 30岁前真的不要进厂打工,否则你会后悔当初的选择有多么愚昧! 你知道吗?如果你30岁之前进工厂打工的话,你一定...

147
《Produce 48》公开导师名单 Wanna One编舞家在内 《Produce 48》,预计6月播出 今日选秀节目《Produce 48》进行了首次录制,与先前《Produce 101》不同的是,这次共有96名分别来自于韩国、日本...

160
中国002航母下海试航,可搭载48架舰载机,战斗力提升了数倍 4月23号对于中国海军来说是一个盛大的日子,同时也是中国双航母的开端。有军迷表示,虽然002航母是中国自主研制的第一...

162
在未来战争中的几大趋势 1.太空战 众所周知,太空站是未来战争中的新制高点。可以说,哪一个国家掌控了宇宙,它便掌控了地球。现如今,太空竞争的形式愈演愈烈,而太空战略的威...

181
唐嫣早期真实素颜照片,唐嫣早期的牙齿不整齐 唐嫣和罗晋的婚礼再一次登上热搜,两人高调的在微博宣布:“新郎是我”“新娘是我 ”的标识,并配上九宫格的照片,再度撒糖。从...
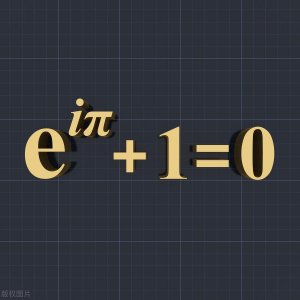
197
什么是欧拉公式? 欧拉公式 是一个数学公式,表示为 e^(ix) = cos(x) + i*sin(x)。它是由欧拉提出的,是复数数学和微积分学的重要公式之一。 首先,欧拉公式的两边都是复数的指数形式。...