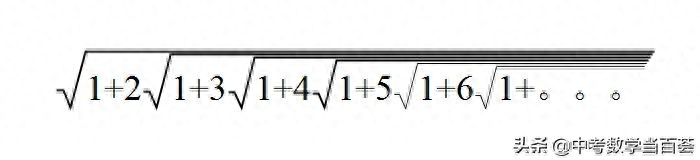拉马努金恒等式，一个初中生能看懂并能证明的神奇公式
拉马努金恒等式，一个初中生能看懂并能证明的神奇公式
-01-拉马努金恒等式
2016年4月8日在英国上映了一部名叫《知无涯者》的电影。电影讲述了印度数学家斯里尼瓦瑟·拉马努金（1887.12.22~1920.4.26），
短暂而传奇的一生。拉马努金出生贫寒，没有受过专门的数学训练，但天资聪颖，完全靠自学。直到1913年，得到英国数学家哈代的赏识，他的数学才华大放异彩。但他不同于传统意义上数学家，他的成果往往是凭直觉得到，只有结论，而没有证明。他短暂的一生发现了3900条数学公式和命题，许多结果完全是新颖的、原始的和非传统的，但被后续证明他的结论都是正确的。
本文要介绍的这个恒等式，就是拉马努金流传最广的成果之一。先看这个恒等式的一边：
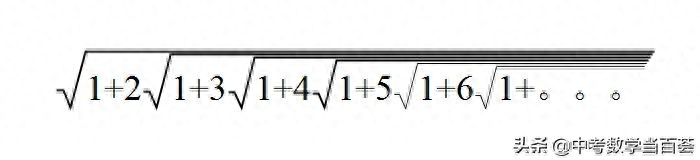
我相信大多数人能按照这个式子的规律接着写下去，但会发现这是无穷尽的，并且很好奇这个式子的结果到底是多少？
拉马努金说，这个式子的结果等于3。
他对形如上式的无穷二次根式，进行深入研究得到这个结果，并且将此发表在《印度数学会刊》上征集证明，数月内无人能应。
-02-拉马努金恒等式的数学逻辑
下面我们以今天中学生的认知来看其中的数学逻辑：
3=√9。。。。。一层根号
=√1+8
=√1+2x4
=√1+2√16。。。。二层根号
=√1+2√1+15
=√1+2√1+3x5
=√1+2√1+3√25。。三层根号
=√1+2√1+3√1+24
=√1+2√1+3√1+4x6
=√1+2√1+3√1+4√36。四层根号
。。。。。。
由此不难发现：将3拆分后，含n层根号时，3=
√1+2√1+。。。n√（n+2）²
。。。n层根号
验证一下，n=10时（由外向内数，含10层根号），壮观景象：
第10层根号里的数：
12²=144；
第9层根号里的数：
11²=121；
第8层根号里的数：
10²=100；
。。。
第3层根号里的数：
5²=25；
第2层根号里的数：
4²=144；
第1层根号里的数：
3²=9；
√9=3
理所当然是个恒等式。
-03-拉马努金恒等式的数学证明
问题来了，正整数3可以象这样用二次根式进行无穷拆分，那么其他正整数呢？他是怎么想到了呢？
平方差公式是初中代数中的最基本的公式之一：
a²-1=(a-1)(a+1)；
变形得
a²=1+(a-1)(a+1)；
即
a=√1+(a-1)(a+1)。
建立一个关于a的函数：
F（a）=a=√1+(a-1)(a+1)，则
F（a+1）=a+1
=√1+(a+1-1)(a+1+1)
=√1+a(a+2)
=√1+aF(a+2)，
F（a+2）=a+2
=√1+(a+2-1)(a+2+1)
=√1+(a+1)(a+3)
=√1+(a+1)F(a+3),
F（a+3）=a+3
=√1+(a+3-1)(a+3+1)
=√1+(a+2)(a+4)
=√1+(a+2)F(a+4)，
...
F（a+n）=a+n
=√1+(a+n-1)(a+n+1)
=√1+(a+n-1)F(a+n+1)，
...
通过层层嵌套，得到
F(a)=√1+(a-1)F(a+1)
=√1+(a-1)√1+aF(a+2)
=√1+(a-1)√1+a√1+(a+1)F(a+3)
...
=√1+(a-1)√1+a√1+(a+1)√1+(a+2)√1+。。。
即
其中，a为正整数。
当a=2时，得到
当a=3时，得到
当a=4时，得到
由此，可以把任意一个正整数，用二次根式有规律地无穷展开。
所以拉马努金恒等式，更一般的形式是：
-04-结语
利用平方差公式和函数嵌套（复合函数）的思想，可以来说明他的正确性。虽然初中不提函数嵌套（复合函数）这种说法，但“整体思想”已经具备其雏形，所以上述证明过程，数学程度稍好的同学也可以看懂。
拉马努金没有受过正规的高等数学教育，但他靠自学沉湎于数论，尤其钟爱涉及π、质数等数学常数的求和公式和整数分拆。特别是他对数的直觉（数感）常常令人称奇，以至于亦师亦友的哈代感叹说：“我们学习数学，拉马努金则发现并创造了数学。”
标签：
187
黄婉秋：因演刘三姐遭批斗险些被枪毙，老百姓都看哭了，但我无悔 一提 《刘三姐》 人们忘不了刘三姐与阿牛哥在大榕树下的山盟海誓，更忘不了主题曲 《多谢了》： “多谢了，多...
130
《权力的游戏》：那些消失后再也没有回来的角色到底发生了什么？ 我们都知道，《权力的游戏》是一部奇幻剧，这部剧非常善于将故事、线索、人物交织在一起，而里面还有着数不清...
99
中国新说唱：小丑频频抱头痛哭，愿赌不服输被所有选手diss 他来了，他来了，他真的来咯。 7月5号《中国新说唱》第四期准时来咯，不出所料，整个节目的气氛和呈现出来的效果依然...
134
心理学家：判断一个人的气场强不强，看看他的房间就知道 每天耕耘最有趣、最实用的心理学 我们常常可以听到周围人对他人会有这样的描述：“这个人的气场很强大。” 那究竟，什...
62
神奇的面包树，一棵树养活一家人，果实味道似面包，还能治病 我们常用“天上掉馅饼”来比喻不切实际的白日梦，可你听说过“树上长面包”么？ 别说，“树上长面包”倒是真的有...
166
提醒一句：饮酒过后出现这5个症状，也许是胰腺炎“悄悄”找上你 胰腺炎是胰腺组织的炎症性疾病，有急慢性之分， 而诱发胰腺炎的危险因素有胆囊结石发展，长期过量饮酒等。 病情...
92
所有人注意！梅子酒再好喝，也千万不要再喝了 不少朋友都会自制一些梅子酒来喝，制作的方法比较容易，而且口感非常好，所以不少朋友都非常喜欢，梅子酒非常好喝，而且营养价格...
76
使用荣耀8x手机的优缺点 荣耀8x已经用了近两个多月了，目前把所有的优缺点归纳已下几点: 优点:1、显示屏幕大，荣耀8X采用6.5英寸的LCD屏幕，色彩鲜艳，并且通过德国莱茵护眼模式，...
188
立定跳远为什么跳不远？又该怎样有针对性的解决？看这里 立定跳远作为体育必考项目之一，直接反映下肢的爆发力和弹跳力，考验全身的协调性、平衡性和灵敏性。 很多人对立定跳...
191
咳嗽-拔罐的部位和方法 一，咳嗽辨证分型： （1），外感咳嗽 1，风寒束肺：咳嗽白痰，鼻塞流涕，恶寒发热，头痛，全身酸楚，舌淡，苔薄白，脉浮紧。 2，风热犯肺：咳嗽黄痰，粘...
83
建设全速推进！淄博341个项目完成投资578亿元 齐鲁网·闪电新闻10月18日讯 10月18日，淄博市政府新闻办公室组织召开新闻发布会，淄博市发展和改革委员会发布了今年以来全市重大项目...
199
火凤凰”黑猫“44岁徐洪浩和34岁的妻子刘晓洁近照，儿子已7岁 徐洪浩，1973年10月28日出生于安徽省合肥市，1996年毕业于上海戏剧学院表演系，中国大陆男演员，徐洪浩在电视剧《DA师...
116
陈全林：93岁老党员的初心本色 为什么入党？ 这是每名共产党员终其一生都要常问常省的命题。入党，是一名党员在灵魂最高处作出的政治抉择，是心灵最深处刻下的精神誓约，更是人...
167
陈情令：魏无羡如何度过乱葬岗的三个月，只道一言难尽 陈情令中，魏无羡剖了自己的金丹给了江澄，灵力尽失的他被温晁丢入乱葬岗，三个月后重归于世。相信很多令牌和小编一样，...
115
朝秦暮楚这个典故的由来到底是什么？ 现在说起朝秦暮楚，肯定有人很熟悉，意思和朝三暮四相近，主要用来比喻人反复无常，没有原则。亦比喻行踪不定或生活不安定。但是关羽朝秦...
177
五经主要内容是什么？ 《文心雕龙.宗经2》作者：刘勰（约公元465——520），字彦和，生活于南北朝时期的南朝梁代，中国历史上的文学理论家、文学批评家。汉族，生于京口（今镇江...
138
如何煮冻饺子，记住这6点，煮熟和鲜水饺一样 饺子很多人爱吃，特别是北方人更爱吃，一个星期不吃上一回，那都要馋坏了，可是包饺子有些太麻烦，费时又费力，现在很多人都很忙...
61
清明节吃什么传统食品 明天就是传统节日清明节了，唐宋之后，清明节就有了追远祭亡、郊游踏青、插柳拔河，放飞纸鸢的传统活动。 不过在今天，清明文化留给我们最深的印记，还...
66
感恩对我好的人的句子（感恩所有帮过我的人的表达） 人活着，不是你认识多少人， 而是你落魄的时候， 有多少人认识你； 人活着，不是仰望你的有多少人， 而是你坠落的时候， 有...
168
肝胆相照的意思是什么 中医药文化│成语中的中医药 肝胆相照 清代小说《儿女英雄传》第十六回中说：“我两个一见，气味相投，肝胆相照。” 肝胆相照是我们耳熟能详的一个成语，...