正态分布(了解正态分布，你看世界的眼光会截然不同)

文/老余

如果你上学时很讨厌数学，我劝你放下这种情绪。

因为如果缺了这一块，很多事没做成就会大概率归结到两个原因，要么是觉得自己努力不够，要么是觉得运气不在我这边，是天要亡我。但如果具备一些数学思维，你就会看到第三种原因：

——不是我不够努力，不是天意如此，是数学模型早就主导了事情的结果。

毕竟，数学规律是这个宇宙的通行证。

本篇是数学思维的第11篇，说一说我们都熟悉的「正态分布」，很有意思。

从我小区楼下的一个小餐馆说起。

昨天到这里吃饭，老板和我也熟，说疫情结束的这一段时间生意比以前好了，好些时候顾客还需要排队，有的等不及就走了，刚好旁边的小店关张了。

问：扩大店面是否可行？

我脑阔里立马就出现了「正态分布」，于是回问了他几个问题：

没有疫情时，店里平均每天大概有多少人（均值）？答：80人左右；

没有疫情那会儿生意好时，能到多少人（算标准差用）？答：100左右吧，但这几天都快到160了；

除了春节，在疫情之前最差的的时候一天大概多少人（算标准差用）？答：60多点；

这几天客人多了，是因为您的菜品有更新吗（其他因素）？答：我最拿手的菜全在菜单里了，没有加其他新菜。

我知道周边也没有新的写字楼等因素导致这里人流量突然加大，

听毕我就给老板说最好不要扩张，这几天的客人陡增多不是常态。

怎么说？

接下来详细说说我的理由，顺便给朋友们复习下相关概念及在生活里的应用，具体讨论三点：

啥是标准差？

啥是正态分布？什么样的事符合正态分布规律？

正态分布能给我们哪些启发？

（一）啥是标准差？

没办法，为把上面的问题讲清楚，就得用正态分布，而要把正态分布搞明白，我们首先要了解什么是标准差。

枯燥的数学概念就不说了，我们直接拿上面餐馆的例子来说。如下图：

标准差怎么理解呢？

简单理解，如果标准差很大，说明这段时间到店人数极不稳定，反之就是到店人数较为稳定。

那为何要先平方后又开方呢？这不是多此一举，因为有些时候的到店人数比平均数小，如果不平方就会有负数出现，这样就达不到描述是否稳定的效果。

这段很无聊，希望你还在看，精彩的在后面。

（二）啥是正态分布？什么样的事符合正态分布规律？

符合正态分布的数据曲线你应该还记得，就是一个“钟型”，如上图。这些数据有什么特点呢？

很有意思：

68.27%的数据会落在平均数±一个标准差之内；

95.45%的数据会落在平均数±两个标准差之内；

99.73%的数据会落在平均数±三个标准差之内。

一脸懵，这是啥？

我们回到小餐馆的例子你就明白了，到店顾客的平均数是80人，标准差我们算出来了，是13.95人，为了直观就看成是14人吧。

就是说，如果这个店已经稳定，没有因为菜品的刺激和写字楼增多的因素，就这么经营下去的话，在以后：

68.27%的日子里，进店用餐的人数会在80±14人之间，也就是66-94人之间；

95.45%的日子里，进店用餐的人数会在80±28人之间，也就是52-108人之间；

99.73%的日子里，进店用餐的人数会在80±42人之间，也就是38-122人之间。

——这就是符合正态分布事件的数据概率分布，是不是有种冥冥中自由定数的感觉？

老板讲这几天人数在160人左右，出现在三个标准差之外的好时光的概率，是0.27%。

也就是说，平均下来差不多一年会遇到这么一天。

为了扩大店面，那岂不是要亏肿？！

在我们的日常生活里，很多事都在正态分布的框架之下，那什么样的事儿归正态分布管？也就是满足什么条件就是正态分布了呢？

具备以下三个条件，就无疑是了：

它是由≥20个随机变量相加的结果（店里来的客人数量满足这一条件，相乘是对数正态分布）；

这些变量是相互独立的（也就是不相互影响，进店顾客是自己决定的，所以也满足这一条件）；

方差有限大（方差是13.95，所以满足）。

爱因斯坦说：

疯狂就是每天重复做同样的事情，却期望得到不同的结果。

如果你做的事已经是稳定的常态且符合正态分布的那三个条件，那么：

——不做出实质性的改变，是不可能出现更好的结果的，严谨一点说，出现“天降横财”的结果概率非常非常小。

我也想了，楼下小店这几天会有这么大的量，如此极端的概率连续出现的原因：应该是周边其他餐饮店因疫情倒闭的太多了，但因为那只“看不见的手”，这个店的竞争马上会多起来，以前的竞争平衡很快就会到来。

——小店很快就会回到正态分布的“控制”之中。

除了以上，正态分布能给我们哪些启发呢？

其实很深刻，我们继续聊。

（三）正态分布给我们的一些启发

对我来说，起码有如下两点：

1、成为高手的过程，就是缩小标准差的过程

那些已经取得过好成绩的运动员每天还是不停的训练，为什么？

我们都知道，是为了维持自己的状态，让自己的成绩保持稳定。如果把这句话换成数学语言，就是为了减少随机独立因素对他的影响，让成绩的标准差尽量小。

再看那些顶尖的管理者（不是酒桌上下属不喝酒，就扇人耳光的那种），他们给下属的指令永远都是「可预测的」，做人做事的标准很清晰，也就是说在员工眼里，BOSS做决策的标准差很小。

这可能与很多人的理解相反，做领导不是要深不可测吗？不是要让人看不懂吗？这是宫斗剧看多了，在真实的商业世界里，领导的决策标准要是不统一、捉摸不透，员工们的动作就会乱掉，因为他们无法预测自己的行为是得到奖励还是惩罚。

于是，员工为了自保，最好的策略就是不动。

这样的企业能好？

我不信。

所以好的领导者，都是标准差很小的人。

作为个体，我们想要与其他人深度合作，想要拿到超额利润，对方最看重我们什么素质，是我们出价比别人低吗？

明白人看重的都不是出价最低者，看的是：

——你是否靠谱。

而靠谱的本质，就是你受情绪、环境影响小，也就是你做人做事标准差很小很稳定，这样对方就很放心与你合作，因为他知道结果差不到哪里去。

这也是为何奈飞公司文化里“只招成年人”的原因。

2、如果想超越阶层，你要逃开正态分布的行业

正态分布出现极端情况的概率很小，也就是说，你要是在正态分布规律的行业里做事，想要出人头地的机会就很渺茫，大概率就是中不溜，饿不死富不了的状态（当然，极度穷困的概率也很小）。

那从分布模型的角度看，如何才能出人头地呢？

秘密就藏在正态分布的第二条里——“这些变量是相互独立的”。

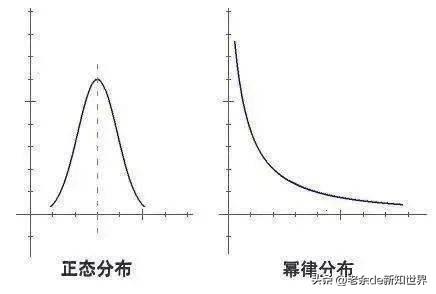
如果把这一条变为不相互独立，那曲线就不是正态分布了，而是幂律分布，这个分布的特点之一就是：

——极端事件很多！

换成人话：

餐饮业之所以巨头很少，相对于其他行业不容易出现巨无霸（极端事件），是因为其最重要的生产要素——人与人之间是独立的，这是一个符合正态分布的行业。

除了餐饮，任何以劳动力为主要生产要素的行业，都符合正态分布，如美容美发、健康医疗等。

所以在这些行业里出现巨无霸是很难的。

而符合幂律分布的行业就不一样了，其主要生产要求之间关联性非常强，甚至有些是相乘的关系，比如以资本和科技为主要生产要求的行业就是如此（互联网、金融、科技等行业）。

这些行业因为符合幂律分布的条件，所以极端事件就很多、且大。

2022年餐饮巨头百胜用了44万人完成营收649亿，而华为2022年的营收是6368亿，是百胜的十倍，但员工不到百胜1/3。

这，就是正态分布与幂律分布的差距。

所以，如果你还年轻，还有选择的机会，最好选幂律分布的行业，这里出现极端巨头的概率大。

或许，你就是下一个豪门。

谁知道呢？