欧拉公式最简单解释(数学界最著名、最伟大、最美丽的公式之一——欧拉公式)

在这篇文章中,我们将探索欧拉公式,解释它是什么,它从哪里来,并揭示它神奇的性质。
欧拉公式是什么?
欧拉公式是欧哈德·欧拉在十八世纪创造的,是数学界最著名、最美丽的公式之一。之所以如此,是因为它涉及到各种显然非常不同的元素,比如无理数e、虚数和三角函数。
让我们看看它是什么样的:
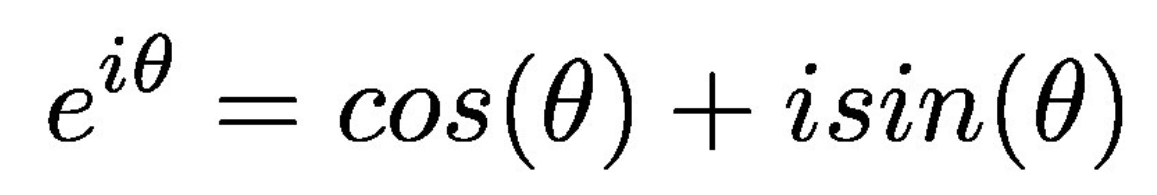
欧拉公式
正如我们所看到的,左边是e,右边是cos和sin三角函数,两边都有虚数i。在我们从微积分和几何的角度研究这个公式之前,让我们先看看这个疯狂的关系是从哪里来的。
欧拉公式的历史
1714年,英国物理学家和数学家罗杰·柯茨在一个公式中建立了对数、三角函数和虚数之间的关系。
二十年后,莱昂哈德·欧拉用指数函数代替对数得到了同样的公式。柯茨的公式如下:
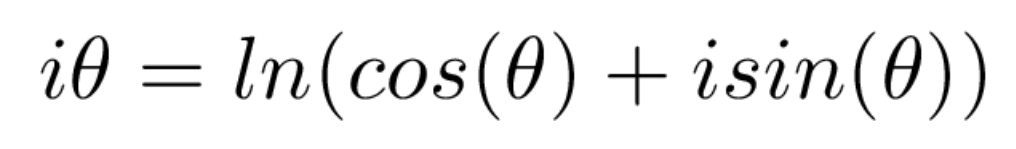
罗杰·柯茨公式
从柯特公式到欧拉公式我们只需要在两边都应用指数。为了将欧拉公式转化为柯特公式,我们用对数反转这个过程。
奇怪的是,每个公式的作者都没有看到它的几何含义,而这正是从这些公式中可以得到的最令人着迷的东西之一。下图展示了一个复平面,我们将在这里看到这些几何内涵。
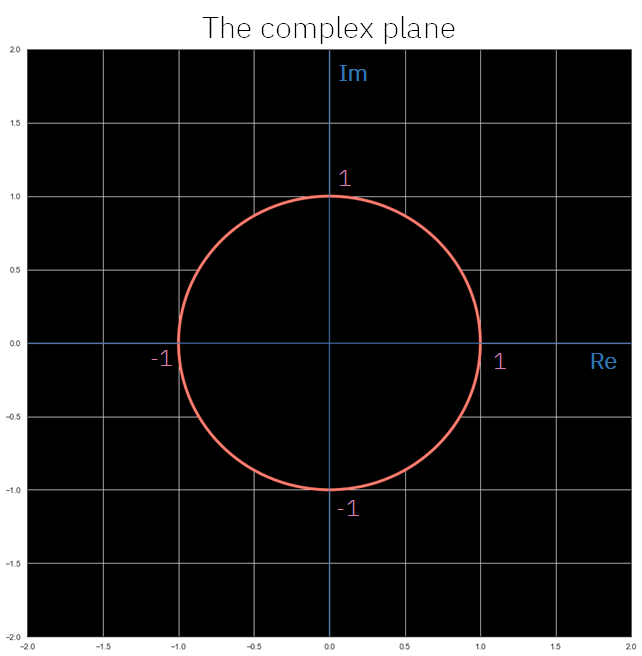
复平面,周长为1
在此之前,你应该知道,如果我们把欧拉公式的值特殊化为:θ= π,我们得到了著名的欧拉恒等式。
欧拉恒等式
如前所述,如果我们设θ= π,欧拉公式就变成了欧拉恒等式。
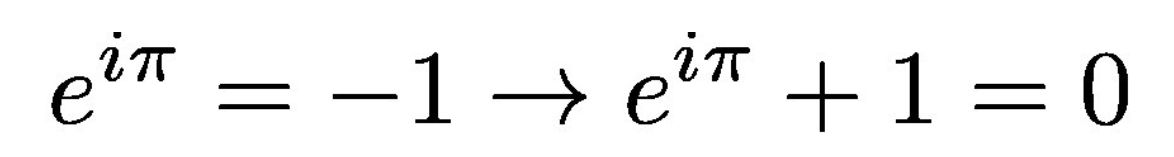
现在我们知道了欧拉公式和欧拉等式是什么,让我们把前者分解成单独的元素,然后探究为什么它是一个如此神奇的方程。
余弦和正弦
正弦和余弦是周期为2π的三角函数。这意味着每2个π它们都回到相同的值。下图显示了这些函数:

sin(左)和cos(右)函数
如果我们看一个直角三角形,角的正弦和余弦可以用这个三角形的边长来计算,像如下图所示:
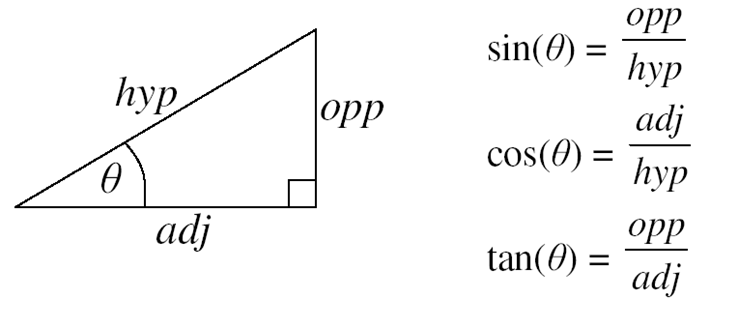
利用直角三角形的边长计算余弦和正弦的值
虚数
最初,人们发明数字是为了记录整个物体的数量,这就是自然数的概念。然后,需要一种机制来跟踪某人何时欠了另一个人整件物品。整数诞生了,它是自然数向负数的延伸。
在此之后,需要跟踪整个对象的部分,从而产生了有理数。最后,在数学中发现了描述分数的数字,这些分数的小数部分永远存在,于是无理数诞生了。前面所有的数字都属于实数的范畴。
但虚数的性质完全不同。虚数一诞生,就被认为是一种数学工具用来处理负数的平方根。i——表示虚数的字母,等于-1的平方根:
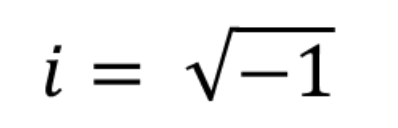
虚数i的值
直到欧拉出现,才用这个字母表示-1的平方根,并开始被认为是通用的。此后,它自然出现在各种物理问题中,如电磁定律,或波动动力学。
无理数e
数学常数e是数学中最重要的数字之一。这个常数,尽管它的名字来自欧拉,有时也被称为欧拉数,在这位著名的数学家推广它之前就被发现了。
具体来说,它是由著名的雅各布·伯努利于1683年在研究复合效应和关于投资随时间指数增长的不同计算时首创的。从这个角度,著名数e计算为:
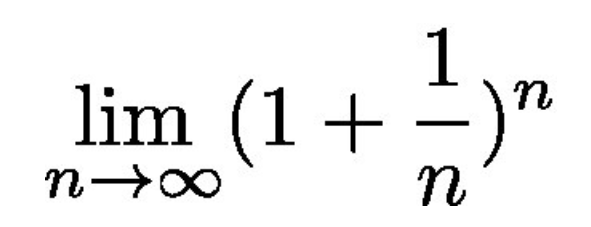
e的计算
这个极限收敛,都知道值约为2.71828。
尽管这个常数非常重要,但欧拉公式的魔力并不是来自这个精确的值,而是来自这个字母的名字所窃取的函数——指数函数。
指数函数
欧拉公式和实数
指数函数的一般概念是重复乘法:
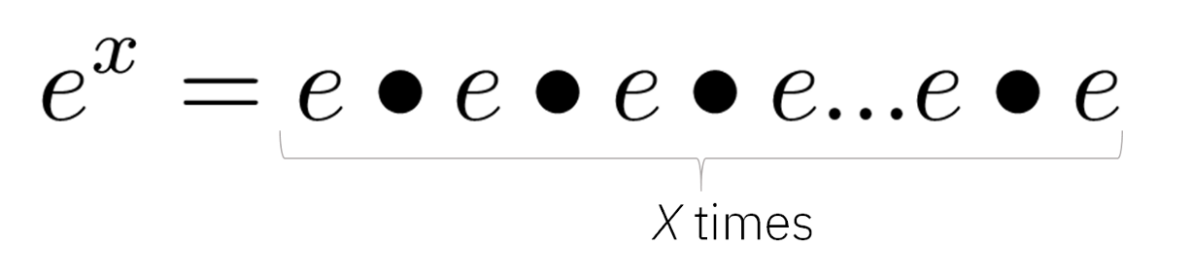
重复乘法
但是,当我们想到指数是一个平方根,一个负数,一个分数,或者一个虚数时,会发生什么呢?重复乘法的概念不再适用。只有当指数为正整数时,它才成立。
指数函数更精确地定义为以下级数,即著名的泰勒级数之一,我们称之为exp(x):

再说一次,尽管这个级数看起来是无限的,但它是收敛的,因为每个分数的分母比分子增长得快得多,而且这个函数本身有一些惊人的性质让我们能够解释分数指数和负指数的值。
我们知道e的值约为2.71828,是当我们把x = 1输入这个指数函数时,得到exp(1) = e。
这个函数最基本最神奇的性质是输入的乘法等于输出的加法:
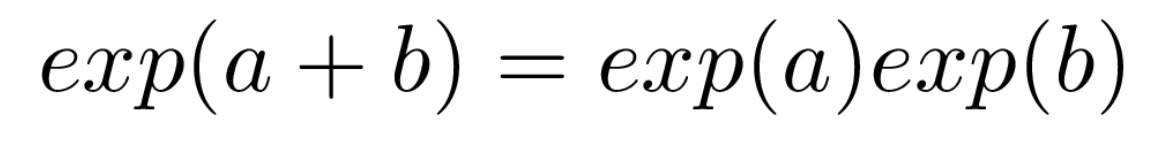
输入相加等于输出相乘
你自己试试吧。得到一个计算器和计算以下:
exp (3) = 20.0855 epx (4) = 54.5981 exp (3) exp (4) = 1096.6331 exp(3 + 4) = exp(7) = 1096.6331
这一点都不平凡,可能没有人会通过看泰勒级数就猜到它。然而,这是一个很棒的性质,它允许我们回答前面的一些问题。
1.将一个数取幂为1/2意味着计算该数的平方根。怎么会这样呢?我们用指数函数之前的性质来计算。
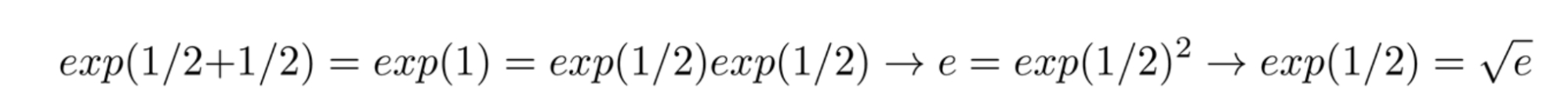
指数分数
exp(1/2 + 1/2)等于exp(1)也就是e。exp(1/2 + 1/2)也等于exp(1/2)exp(1/2)。所以exp(1/2)²等于e因此exp(1/2)等于e的平方根。
2. 将一个数取幂为0等于1。这要归功于多项式泰勒级数当x = 0时。
3.将一个数取幂到-1等于1除以那个数。只要知道exp(0) = 1就可以很容易地推导出来。
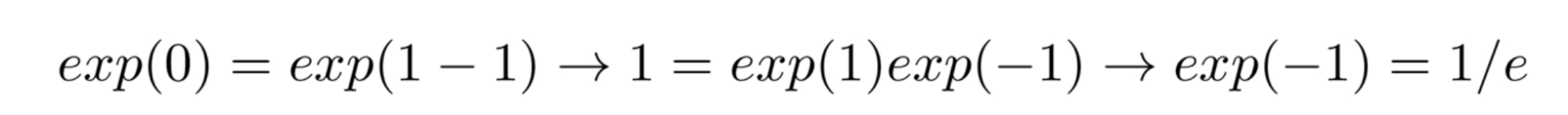
一个负数的指数
现在,当我们在exp函数中插入一个虚数会发生什么呢
欧拉公式和复数
要想看到这样做的结果,我们需要回到复平面。让我们计算单位圆上的复数,用粉色表示。
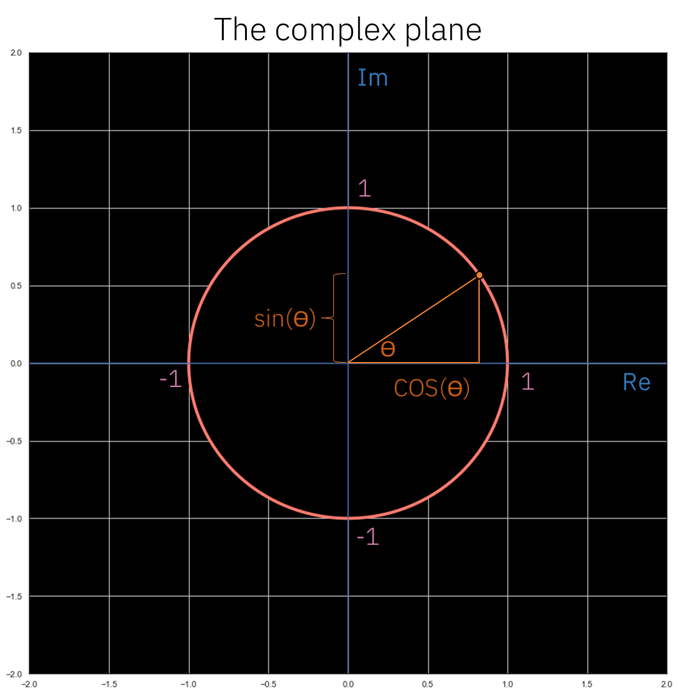
复平面
假设我们有之前的虚数,用欧拉公式描述并在复平面中用橙色点表示。
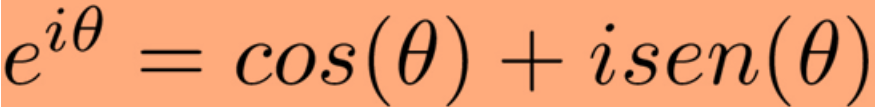
如果我们给指数函数一个虚数作为参数,会发生什么?exp(i θ)是什么?
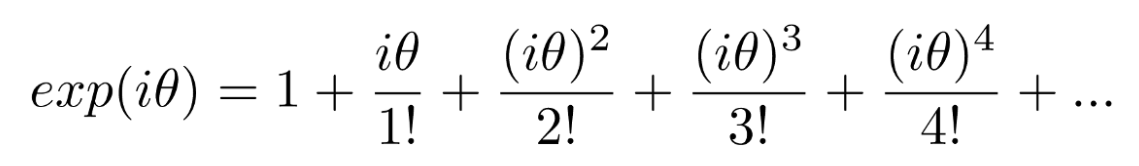
i θ的指数函数的前四个元素
让我们选择一个特定的值,看看会得到什么。取θ = 1,计算exp(i)的前20个元素,得到复数:0.5403 + 0.8414i。这和我们从欧拉公式中得到的值是一样的。
很有趣的是,随着在泰勒级数中加入越来越多的相,这个计算就变得更加精确了,几何上是怎么做的。下面的列表显示了,当我们考虑到前面系列中越来越多的项时,exp(i)的值是如何变得越来越精确的。
泰勒级数中有1项的exp(i)值:1 泰勒级数中有2项的exp(i)值:1 + i 泰勒级数中有3项的exp(i)值:0.5 + i 泰勒级数中有4项的exp(i)值:0.5 + 0.83333i 泰勒级数中有5项的exp(i)值:0.541666 + 0.83333i 泰勒级数中有6项的exp(i)值:0.541666 + 0.841666i 泰勒级数中有7项的exp(i)值:0.5402777 + 0.841666i 泰勒级数中有8项的exp(i)值:0.5402777 + 0.841468i 泰勒级数有9项的exp(i)值:0.5403025 + 0.841468i
现在,让我们看一些更酷的东西。下面的图显示了当我们增加泰勒级数中考虑的项的数量时exp(i)的值的曲线。每条黄线结束于用这么多元素计算出的复数的值,并表示对前一条的额外添加。
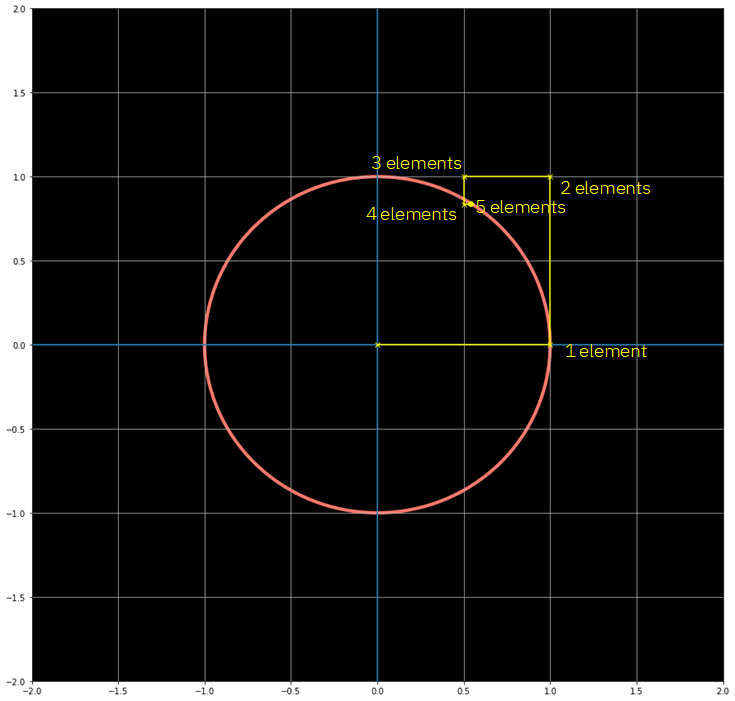
复平面和exp(i)的值。最后,在添加了5项之后,我们可以看到我们非常接近单位圆上的真实值。
我们可以看到,形成了一种螺旋,它越来越接近最终的指数值,我们可以用欧拉公式来验证。这太棒了,它告诉我们一些关于指数的美妙之处。
如果我们使用足够的多项式级数的项exp(iθ) 最终总是在单位圆上,绕着它旋转了一个弧度。
如下图所示,与之前的图相同的是不同的数值。
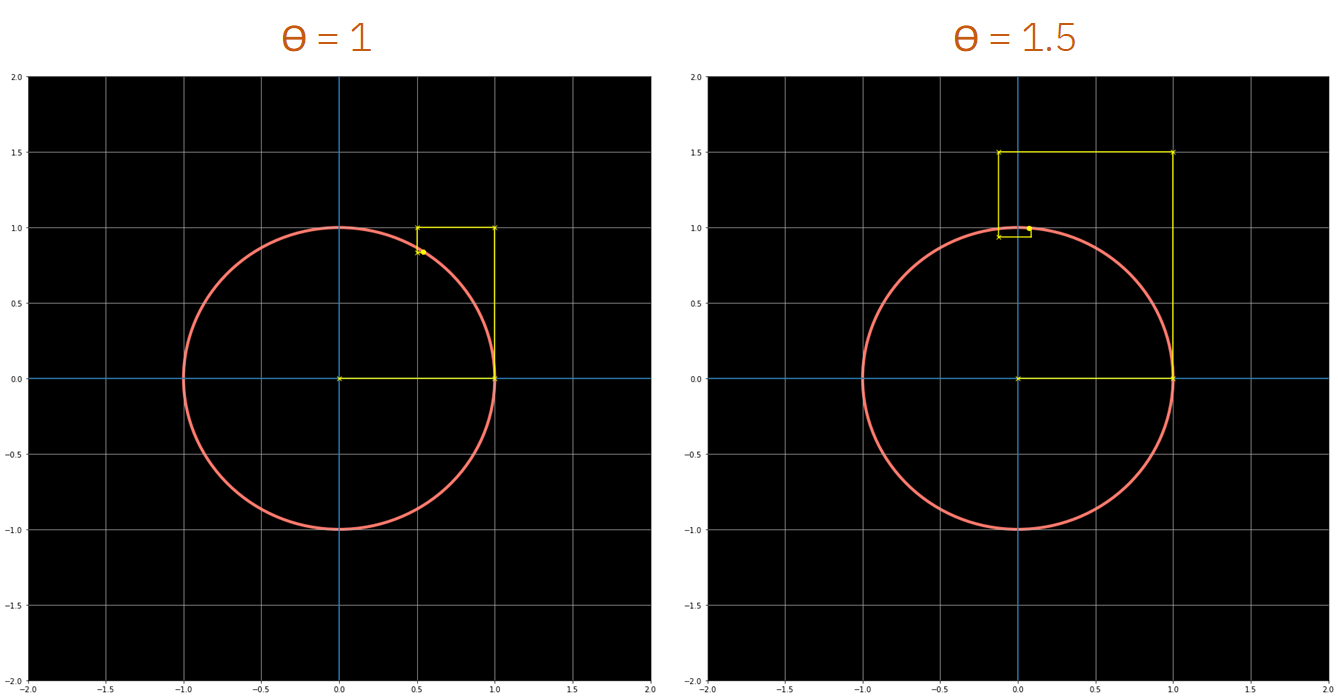
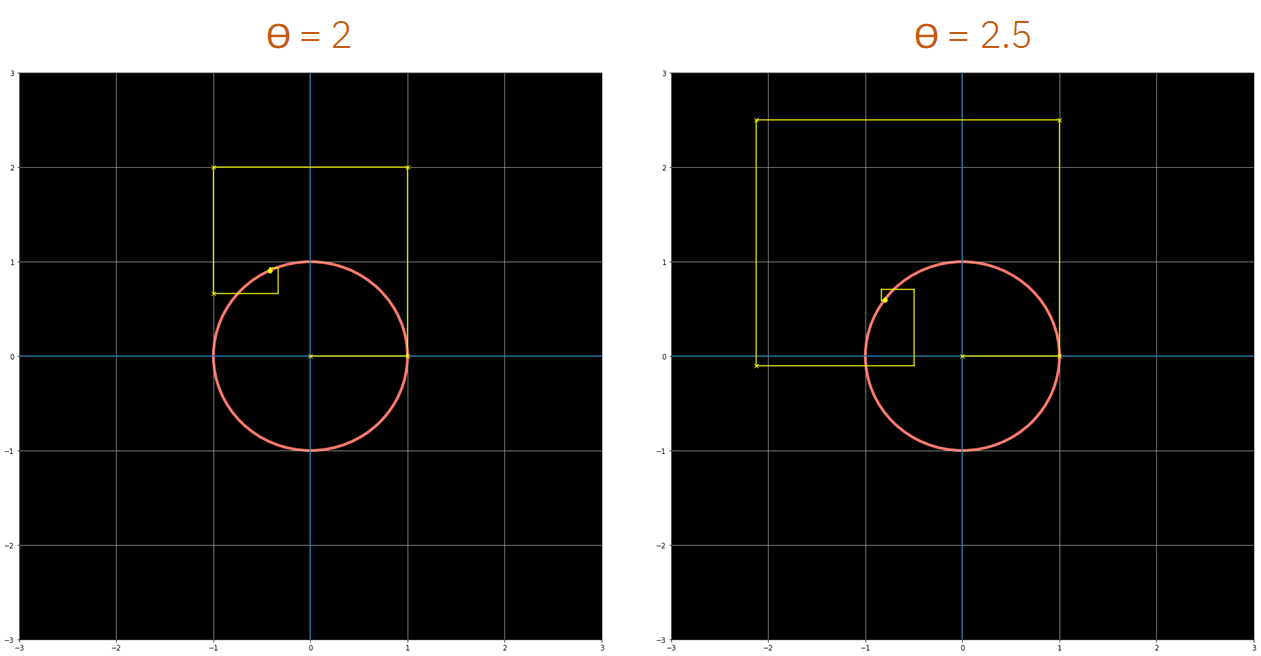

从前面的图中我们可以看到,如果使用了足够的项,exp(iθ) 总是在单位圆中结束。对于任意的值,如果我们在多项式级数中取足够的项这总是会发生的,只要把这些表示级数中额外元素的黄线相加,旋转和相乘就行了。
另外,您可能已经注意到,在最后一幅图中,我们所绘制的是欧拉恒等式。让我们恢复公式,因为这最后的部分也包含一些美丽东西:
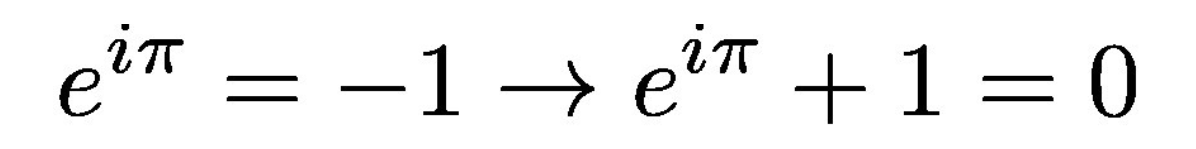
如果我们代入(θ=π),我们得到欧拉恒等式,数学和几何告诉我们:常数e的iπ次方为-1,没有虚部,也就是公式的右边。
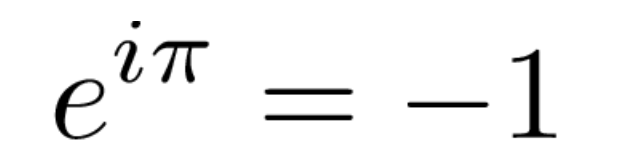
几何上,正如我们看到的,这都是通过旋转向量并乘以它们的长度来实现的。
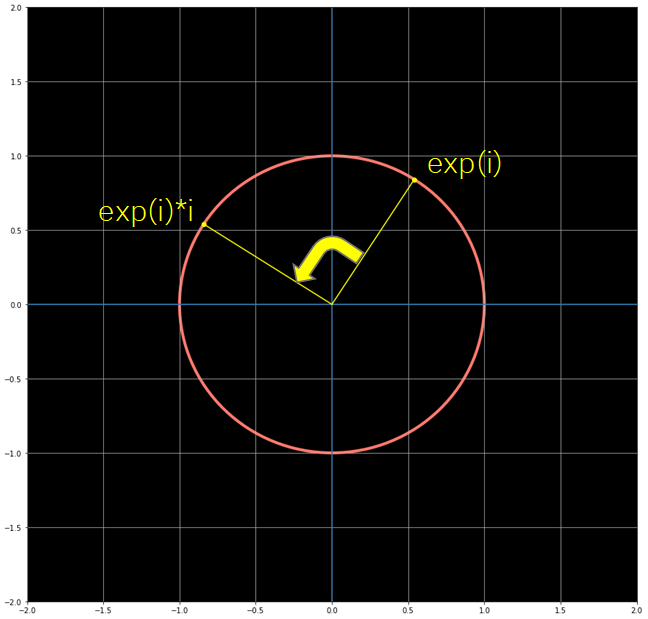
这完全令人困惑!产生这个的一个主要原因是,在复平面上当我们将一个数乘以i时会发生什么。乘以i意味着从原点绕单位圆旋转90º,如下图所示:
结论

欧拉公式是当今最美丽的公式之一。它完美地连接了许多不同的元素,它的几何解释和起源是非常美妙的。这就像大自然试图告诉我们一些事情。
















