木马检测正确方法(基于XGBoost的硬件木马检测方法)
随着集成电路产业的全球化生产策略和电路设计大规模化,IC设计公司很少能从设计到制造独立完成所有的模块设计,更多地是采用第三方的知识产权(IP),或将芯片的生产封装承包给第三方。集成电路在设计、制造、测试以及封装过程中都不完全自主可控,这为攻击者对集成电路实施破坏或恶意修改提供了可能。攻击者可以插入恶意电路到芯片中,破坏芯片功能或降低芯片可靠性,而这种恶意的变更,称为硬件木马。
近年来,国内外科研机构开展了很多针对硬件木马防护的研究工作[1-2],这些研究主要面向检测技术,尤其是旁路信息分析技术。文献[3]和[4]利用了PCA、马氏距离来检测木马;文献[5]提出了基于神经网络的硬件木马检测方法;文献[6]和[7]分别利用了朴素贝叶斯分类器和支持向量机来检测木马。
本文将结合机器学习的分类思想,提出一种基于XGBoost(eXtreme Gradient Boosting)的硬件木马检测方法。将硬件木马检测的多维度向量数据作为训练集,利用监督学习模型对其进行分类,从而实现将标准芯片与被植入木马芯片分离的目的。
1 XGBoost算法与交叉验证
XGboost(eXtreme Gradient Boosting)是GB(Gradient Boosting)的高效实现。GB是一种用于回归和分类问题的学习模型,该模型以弱预测模型集合的形式产生强预测模型。通过每次迭代生成一棵新树,选择指向负梯度方向的弱预测模型,来优化函数空间上目标函数。XGBoost是在GBDT算法基础上进一步优化,在基学习器损失函数采用二阶泰勒展开式的形式并引入正则项,具有不易过拟合、灵活性高、收敛速度快、准确度高等特点,能够处理稀疏特征,支持多线程并行处理。
1.1 集成树模型
集成树是由多个分类与回归树得到泛化的模型,弥补了单棵决策树预测性能局限性。

1.2 梯度提升
对式(2)集成树模型中的目标函数,采用additive training方法训练,即每一次保留原来的模型不变,加入一个新的函数f到模型中。

定义Ij={i|q(xi)=j},将常数项移除且叶节点重新组合后目标函数为:
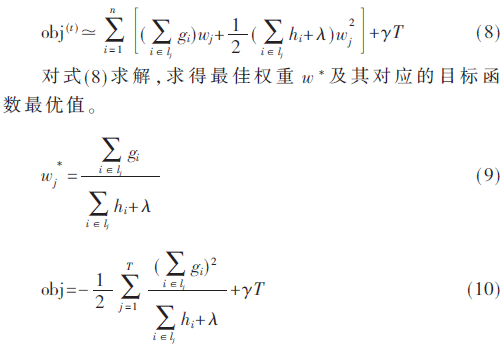
1.3 S折交叉验证(S-CV)
S折交叉验证(Cross Validation)是用来验证分类器性能的一种常用统计分析方法。首先随机地将已给数据切分为S个互不相交的大小相同的子集,然后利用S-1个子集的数据训练模型,利用余下的子集测试模型,将这一过程对可能的S种选择重复进行,最后选出S次评测中平均测试误差最小的模型。
S-CV能从有限数据中获取更多有效信息,一定程度上避免过拟合和欠拟合,更好描述模型数据。在XG-Boost中,采用与scikit-learn框架相结合来作交叉验证。
2 硬件木马检测环境及流程
2.1 检测环境
整个实验平台为一个内嵌9个环形振荡器(Ring Oscillator,RO)的FPGA平台。图1为RO在木马电路上的布局。
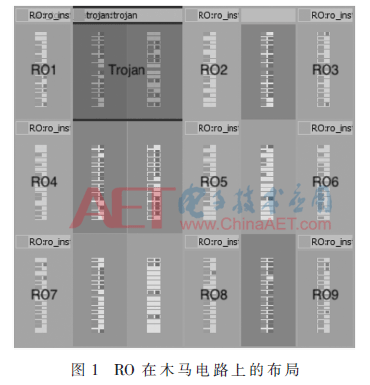
木马电路本身的存在就会对RO输出频率产生一定的影响,不需要处于激活状态,而且当RO的阶数n越小时,RO对木马越敏感,但如果阶数n太小的话,RO输出频率就不能被片上计数器采到,而太大的话,硬件木马的影响就会降低;同样数据采集积分时间理论上来说越长,原始数据与木马数据差异越大,但实际测试中RO积分值会受温度的影响,时间太长会造成积分值变小、区分度减弱。通过仿真分析,本文选用5阶作为最小的RO阶数,且采集时间控制在0.1 ms~0.6 ms范围之内。
2.2 检测流程
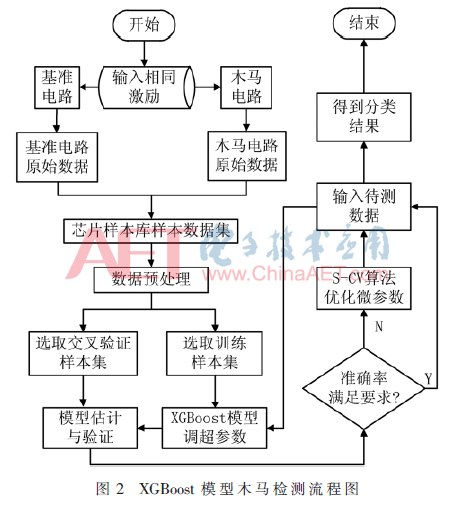
基于XGBoost木马检测模型是利用XGBoost算法对硬件木马检测的多维度特征数据作分类判断的一种监督学习模型。图2为XGBoost模型木马检测流程图。
3 硬件木马检测实验
3.1 实验环境
为了验证提出的硬件木马检测方法,搭建了一个内嵌9个RO的FPGA实验平台。FPGA型号为Altera的EP4CE6F17C8,基准电路采用Trust-hub上的RS232的T100、T800电路。在SMIC 130 nm工艺库下,Design Compiler 综合结果见表1。
根据图2流程分别得到原始数据和木马数据。统计不同位置RO样本点的分布范围,以直观显示数据之间的差异。T800电路在50 MHz下,RO为5阶,采集时间为0.1 ms下不同位置部分RO的数据对比,如图3所示。
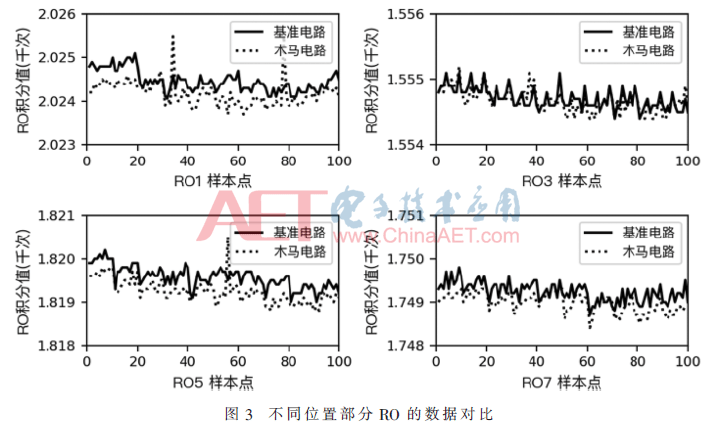
从图中可以看出:(1)不同RO受到木马的影响是不同的,越靠近木马的RO受到的影响越大。虽然原始数据与木马数据有部分分离,但仍有部分重叠在一起;(2)随着FPGA工作时间增加,RO积分值呈下降趋势,这是因为在电路运行过程中,会产生热功耗,会引起温度等环境的变化,RO积分值会受温度的影响。
3.2 实验结果
3.2.1 XGBoost预测结果
对RS232-T800电路,各采集1 000组数据分别作为训练样本和测试样本,经过XGBoost模型训练,分类测试样本准确率只能达到78.80%,分类结果如图4所示,相应模型参数见表2。


3.2.2 XGBoost模型优化结果
针对上述XGBoost模型中诸多重要参数,本文采用S-CV结合高负荷的栅格搜索(girdSearch)方法进行优化选择。
实验验证了上述模型交叉验证方法,根据S-CV算法选择得到的参数见表3。整体log损失值随迭代次数的收敛变化如图5所示。
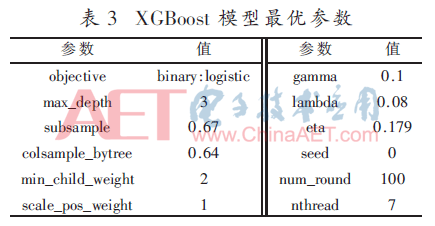
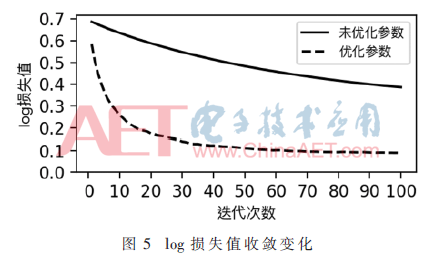
图5中纵轴表示目标函数损失值,横轴表示迭代次数。从图中可以看出,交叉验证参数选择后梯度下降速度更快,且在迭代次数大于60时,损失值稳定范围在0.1左右。实验表明,经过交叉验证参数选择,优化了XGBoost模型,使得准确率从最初的78.80%提高到99.20%,相应地整体logloss值从最初的0.386 303降到了0.089 183。
3.2.3 不同特征下检测结果
为了验证基于XGBoost的硬件木马检测方法的健壮性,作不同特征变化下分类判别实验。表4给出了不同木马面积和不同积分时间下的木马检测结果。
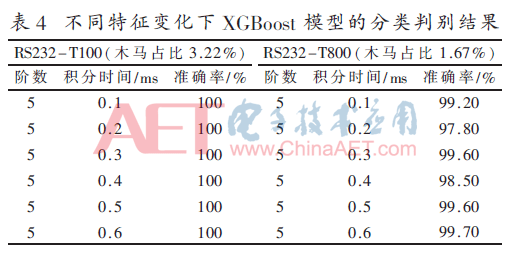
从表中可总结出:(1)该方法能有效检测出1.67%木马占比的电路;(2)对不同积分时间数据仍然保持较强的有效性,准确率能保持在97.80%以上。
4 与其他算法性能对比
在以往的工作中已验证了朴素贝叶斯分类算法、SVM和马氏距离方法的可行性,为验证该方法的优越性,下面给出XGBoost模型与部分现有方法的性能对比。
4.1 与马氏距离算法性能对比
图6给出相同条件下,使用PCA与马氏距离相结合方法马氏距离分析结果,可以看出此判别方法无法有效将基准电路与木马电路分离开来。

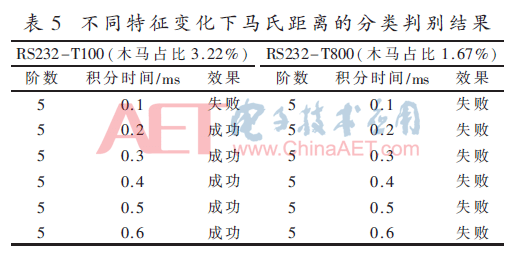
表5给出了不同特征下马氏距离的分类判别结果。对比表4可以看出,在相同条件下,XGBoost模型检测木马的性能明显优于马氏距离判别法,并且马氏距离无法识别数据相差不大和木马占比较小的电路。
4.2 与其他机器学习算法性能对比
在相同条件下,经过SCV算法优化,支持向量机的惩罚参数c=3.1且选择RBF核函数的参数g=6.0时,准确率最高为98.20%,但朴素贝叶斯分类分类只能最高保持在77.40%的正确率上。
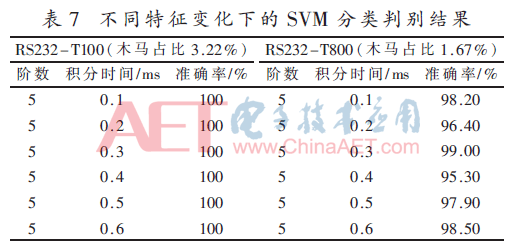
表6、表7给出了不同特性下各算法的分类判别结果。从表中可看出在相同条件下,SVM性能较优于朴素贝叶斯算法,能高准确识别木马数据和原始数据,而与表4作比较,可看出本文所使用的XGBoost硬件木马检测方法能较高准确率识别木马数据和原始数据,相比两者平均准确率高出1.52%、29.2%。

5 结论
本文提出了一种基于XGBoost的硬件木马检测方法,利用S-CV与girdSearch相结合的交叉验证方法优化模型。搭建FPGA实验,验证了该方法的有效性,并在与传统方法和其他机器学习方法比较时,证实了该方法的优越性,更有效地实现木马检测。后续将提出一种工艺偏差的可信空间建模方法,减少工艺偏差的影响。
参考文献
[1] ZHANG X,TEHRANIPOOR M.RON:an on-chip ring oscillator network for hardware Trojan detection[C].Design, Automation & Test in Europe Conference & Exhibition.IEEE,2011:1638-1643.
[2] CHEN T,GUESTRIN C.XGBoost:a scalable tree boosting system[C].ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM,2016:785-794.
[3] 赵毅强,杨松,何家骥,等.基于主成分分析的硬件木马检测方法[J].华中科技大学学报(自然科学版),2015,43(8):66-69.
[4] 王力纬,贾鲲鹏,方文啸,等.基于马氏距离的硬件木马检测方法[J].微电子学,2013(6):817-820.
[5] 赵毅强,刘沈丰,何家骥,等.基于自组织竞争神经网络的硬件木马检测方法[J].华中科技大学学报(自然科学版),2016,44(2):51-55.
[6] 苏静,路文玲,赵毅强,等.基于支持向量机的硬件木马检测建模与优化[J].信息网络安全,2017(8):33-38.
[7] 王建新,王柏人,曲鸣,等.基于朴素贝叶斯分类器的硬件木马检测方法[J].计算机应用研究,2017,34(10):3073-3076.
[8] LECOMTE M,FOURNIER J,MAURINE P.An on-chip technique to detect hardware Trojans and assist counterfeit identification[J].IEEE Transactions on Very Large Scale Integration Systems,2016,PP(99):3317-3330.
作者信息:

















